Talking about us











An artificial intelligence that improves your investment decision making by filtering out the noise, providing relevant information and increasing the probability of success by better understanding the risks involved.
Click on any element and you will be able to interact with the platform

















We can help you figure out how StockFink can help you through a chat where you will speak with Aida, Project Lead & co-founder, and find out how AI can improve your financial freedom.
Schedule a free meetingAn impartial platform, based entirely on artificial intelligence and objective, proven criteria
We transmit data in a direct and accessible way, guaranteeing 100% objectivity
We are here solely for the benefit of our users, with no special interests in mind

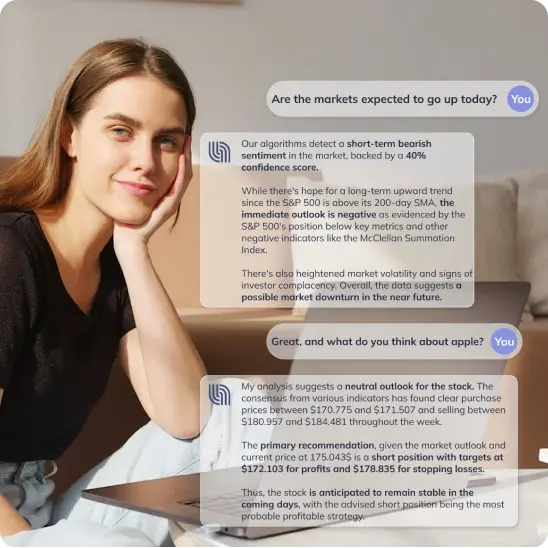
Our algorithms carefully study a large amount of historial data from various markets over many years to discover and leverage repeating patterns. The power of deep neural networks, predictive algorithms, deep learning, natural language processing, and sentiment analysis, among others, all in one platform

CAC
DAX
EUROSTOXX
FTSE
IBEX35
NASDAQ
NYSE
Forex
SP500


Do you want to invest and
Do you want to invest and don't know how to start?
don't know how to start?
It's never too late to invest and one of the things you'll learn in our manual is that the sooner you start the better.
In this small manual we give you:
